How many feet are equivalent to 1.8 meters? Understanding the conversion between metric and imperial units.

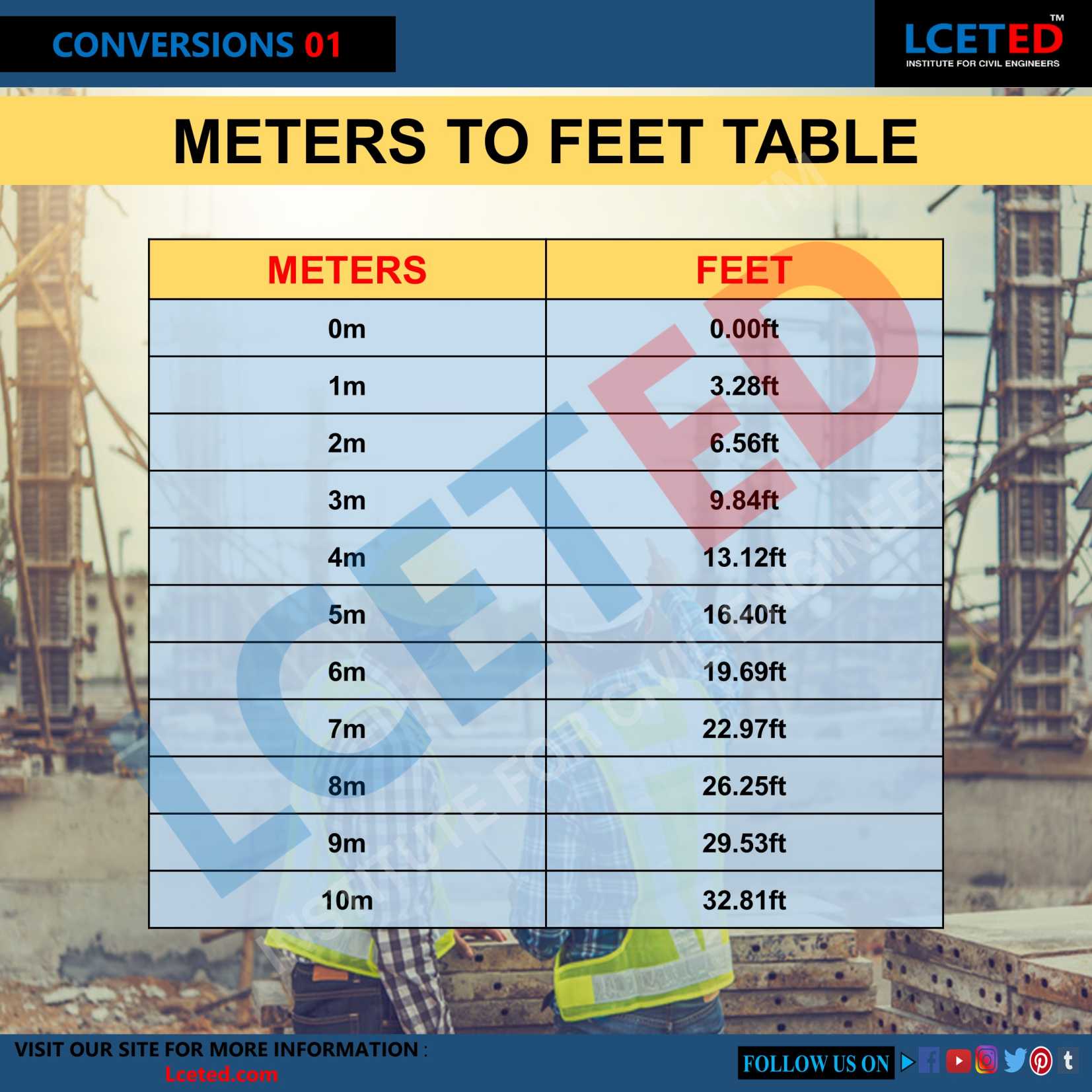
Converting between different units of measurement is a fundamental aspect of various fields, from engineering and construction to everyday activities. A common conversion involves transforming measurements from the metric system (meters) to the imperial system (feet). 1.8 meters is a frequently encountered length measurement. To express this length in feet, the conversion factor of approximately 3.28 feet per meter is applied. Consequently, 1.8 meters is equivalent to approximately 5.904 feet.

The ability to convert between measurement systems is crucial for effective communication and collaboration. In international contexts, particularly in engineering and scientific collaborations, consistent use of a single unit system (typically metric) is increasingly common. However, the continued use of imperial units in some regions necessitates accurate conversion techniques. Understanding and executing these conversions accurately ensures a common comprehension of dimensional quantities, avoiding potential misunderstandings or miscalculations. The conversion process is straightforward, using established conversion factors. This ensures the integrity of measurements and data.

This understanding of converting between meters and feet is a cornerstone in numerous fields. Further exploration into unit conversions and dimensional analysis extends these foundational concepts. This knowledge is applicable to numerous aspects of engineering, physics, and other scientific or technical endeavors.

1.8m in ft

Understanding the conversion between meters and feet is essential in diverse applications, from construction to scientific measurements.

Conversion
Measurement
Units
Equivalence
Approximation
Conversion factors

The phrase "1.8m in ft" signifies a conversion need. Conversion factors (like 3.28 feet per meter) link the metric and imperial systems. Measurement accuracy depends on using these correct conversion factors. The equivalence of these units is critical in various fields. An approximation of 1.8 meters being roughly 5.9 feet is useful for quick estimations. Accurate conversion calculations are vital in architecture, engineering, and scientific analysis, where precise measurements are paramount. For example, a blueprint requiring a 1.8-meter dimension will need precise conversion to feet for accurate application.

1. Conversion

Conversion, in the context of "1.8m in ft," represents the fundamental process of transforming a measurement from one unit system to another. The need for this conversion arises from the coexistence of metric (meters) and imperial (feet) measurement systems. Accurate conversion is crucial in situations requiring compatibility between these systems. For instance, a building design using international standards might express dimensions in meters, while local regulations or building codes might necessitate those dimensions to be expressed in feet. Without a precise conversion method, the design cannot be implemented correctly.

The importance of conversion extends beyond architectural contexts. Scientific research, engineering projects, and everyday applications like global trade often rely on converting measurements. Different countries and regions utilize distinct unit systems. Proper conversion ensures seamless communication and facilitates efficient collaboration. An incorrect conversion could lead to significant errors in construction, product development, or even scientific experiments. In international commerce, the conversion of weights and measures ensures that transactions are fair and accurate across borders. For instance, importing materials from a country that primarily utilizes the metric system necessitates accurate conversions to the imperial system for proper inventory management and pricing within the destination country.

In summary, conversion is an essential component of interpreting and applying measurements across different systems. The conversion of "1.8m in ft" exemplifies the broader need for accurate translations between various units. Effective conversion, built upon a strong understanding of the underlying principles and established conversion factors, safeguards against errors in a multitude of professional and practical scenarios. This ensures accuracy and consistency in diverse applications.

2. Measurement

Measurement is fundamental to numerous fields, acting as a common language for quantifying physical attributes. The concept of "1.8m in ft" directly relates to this, highlighting the necessity of accurate measurement across different systems of units. Understanding the intricacies of measurement is crucial to ensure precision and avoid discrepancies when comparing or applying these values in diverse contexts.

Unit Conversion
The conversion between meters (m) and feet (ft) is a prime example of the importance of measurement units. Accuracy in conversion is vital; an error in converting 1.8 meters to feet could have significant consequences in various applications. Whether it's engineering designs, scientific experiments, or architectural blueprints, the precision of these measurements directly impacts the outcome. Inaccurate conversions can lead to miscalculations, misinterpretations, and ultimately, errors in the final product or result.
Accuracy and Precision
Precise measurement is essential for reliability. A measurement's accuracy reflects its closeness to the true value, while precision describes the consistency and repeatability of the measurement. Variations in measurement tools, techniques, or environmental factors can influence both accuracy and precision. Maintaining high accuracy and precision is critical for all forms of measurement, including converting between units like "1.8m in ft." Such precision ensures that the resulting value in feet accurately represents the original 1.8-meter measurement.
Contextual Understanding
The context surrounding a measurement significantly impacts its meaning. A length measurement of 1.8 meters might be insignificant in a home renovation context but crucial in an engineering design or a manufacturing process. The appropriate units and levels of accuracy depend on the context. Using appropriate measurements ensures the results are relevant and meaningful for the specific task. Conversion of 1.8 meters to feet should be relevant to the application and accurately represent the measurement in its intended context.
Impact on Outcomes
Measurement errors can have cascading effects, affecting subsequent calculations and decisions. Converting "1.8m in ft" correctly is vital for achieving desired outcomes. Inaccurate conversion can introduce errors that might become magnified in calculations. Accuracy and precision in measurement are crucial for all aspects, particularly when dealing with complex systems where multiple measurements are used to achieve a final result.

Ultimately, the conversion of "1.8m in ft" highlights the pervasive role of measurement. Understanding the principles of accurate measurement, units of conversion, precision, and contextual relevance is paramount for obtaining meaningful and reliable results in any field relying on numerical data. Each step in the measurement processfrom initial quantification to final interpretationmust be executed with accuracy and meticulous attention to detail.

3. Units

Units of measurement, fundamental to quantifying physical attributes, form the bedrock of the conversion "1.8m in ft." The very act of expressing a length as "1.8 meters" or "approximately 5.9 feet" underscores the necessity of units. Without these defined units, the numerical value alone possesses no inherent meaning. The choice of units directly influences the subsequent calculations and interpretations of the measurement. This connection is evident in various domains.

The practical significance of understanding units extends across numerous fields. In engineering, precise dimensional specifications, crucial for the construction of structures and machines, rely heavily on consistent units. Discrepancies in units, such as failing to convert meters to feet accurately, can lead to catastrophic structural failures. In manufacturing, consistent use of units is essential for product design and assembly. A component designed using incorrect units results in a non-functional or potentially harmful product. Similarly, in scientific research, accurate use of units is vital for experimental reproducibility and data interpretation. Inaccurate unit conversion can lead to errors in calculations and ultimately, flawed conclusions. Consider the consequences of incorrectly expressing the speed of a chemical reaction, leading to incorrect predictions regarding its outcome.

In essence, the relationship between units and a conversion like "1.8m in ft" is foundational. Understanding units is not merely a technical skill; it is crucial for accuracy, precision, and the validity of any measurement-based analysis or application. The potential for errors arising from neglecting the importance of units is substantial. Therefore, the awareness and consistent application of appropriate units are indispensable for reliable outcomes across various disciplines.

4. Equivalence

The concept of equivalence is fundamental to the conversion "1.8m in ft." Equivalence, in this context, signifies the relationship between two different units of measurement that represent the same physical quantity. 1.8 meters possesses a specific physical length, and its equivalence to approximately 5.9 feet reflects this shared physical reality. A crucial aspect of equivalence lies in its ability to bridge disparate measurement systems, enabling consistent communication and understanding. Without recognizing the equivalence between metric and imperial units, accurate representation of physical quantities becomes impossible across diverse contexts.

The practical significance of this understanding is evident in numerous fields. In architectural design, if a blueprint specifies a dimension in meters, the ability to establish equivalence with feet is critical for accurate on-site construction. In global trade, the equivalence of units ensures fair pricing and the correct physical delivery of goods measured in various units. Equivalence also underpins scientific research; experimental results expressed in one unit must be readily understandable in another, allowing researchers to compare observations and develop theories across disciplines and geographical boundaries. For instance, if a scientific study quantifies the speed of a chemical reaction in meters per second, its equivalence to kilometers per hour is important for broader comparisons and insights. The lack of this understanding can result in misinterpretations, errors, and ultimately, flawed conclusions. Consequently, the ability to recognize and apply equivalence effectively is a fundamental skill across disciplines.

In essence, equivalence serves as a bridging concept between distinct systems of measurement. The relationship of "1.8m in ft," an example of equivalence, demonstrates how conversion from one unit to another preserves the inherent physical quantity. Understanding and applying these equivalences ensures consistent comprehension and avoids ambiguity in various practical and scientific applications. The recognition of equivalence between different unit systems is essential for facilitating smooth communication, accurate calculations, and reliable results.

5. Approximation

The conversion of "1.8m in ft" often necessitates approximation. Precise conversion factors, while theoretically available, may not always be required or practical. Approximation, in this context, involves using a rounded value to simplify calculations or estimations, particularly when dealing with non-critical applications. The degree of accuracy required dictates whether an approximation is sufficient or if precise conversion is necessary.

Accuracy Requirements
The precision needed for "1.8m in ft" directly impacts the necessity for approximation. In a home improvement project where measurements are for general layout, a rounded value might suffice. However, if the measurement determines crucial structural elements, precise conversion is paramount to prevent errors. Different applications require different levels of precision.
Practical Considerations
Real-world scenarios often prioritize practicality. A quick calculation might use an approximate value of 1.8 meters equaling 6 feet for preliminary work, saving time and resources. However, for critical engineering applications, the precise value is essential. Conversion tables and calculators offer varied levels of accuracy, allowing users to adjust precision based on project demands.
Calculation Simplification
Approximation streamlines calculations. An approximate value for "1.8m in ft" simplifies preliminary estimations or quick conversions. Approximation can reduce computational complexity in situations where a high degree of precision is not demanded. The use of approximate values should be carefully considered in conjunction with the overall accuracy needs of the application.
Contextual Awareness
The context surrounding the conversion of "1.8m in ft" plays a critical role in the choice between approximation and precise conversion. In an architectural setting where the overall scale is immense, a slight approximation might be inconsequential. However, for situations involving precise engineering or scientific calculations, exact conversion factors must be used to prevent errors and ensure the accuracy of the final results.

In conclusion, the approximation used for "1.8m in ft" depends significantly on the context and the required accuracy. While approximations streamline calculations in less-critical settings, precise conversion remains essential for applications needing high levels of accuracy. A thoughtful evaluation of these elements ensures that the chosen approach aligns with the needs of the specific application.

6. Conversion factors

Conversion factors are essential components in converting between different units of measurement, such as the transition from meters to feet. The conversion of "1.8m in ft" directly relies on a conversion factor. This factor, representing the fixed ratio between the two units, dictates the precise numerical relationship. Without a known and accurate conversion factor, the translation from meters to feet for a value like 1.8 meters becomes impossible. The application of this factor is fundamental to maintaining accuracy and consistency in measurements, particularly in fields like engineering, architecture, and scientific research.

The crucial role of conversion factors is evident in various real-world applications. Architectural blueprints, for instance, often use metric measurements. Accurate construction necessitates converting these metric dimensions to the local unit system. A significant error in this conversion process could lead to discrepancies in the final structure, jeopardizing both its structural integrity and aesthetic appeal. In global trade, accurately converting units like "1.8m in ft" is paramount for fair pricing, proper inventory management, and the seamless flow of goods across different countries with differing systems of measurement. Similarly, scientific experiments require precise unit conversions to ensure data consistency and comparability across various studies. A mistake in the conversion factor can lead to the misinterpretation of results or inaccuracies in reported values.

In summary, conversion factors are integral to the conversion of "1.8m in ft" and, more broadly, to accurate measurements across different systems. The proper application of these factors is critical to avoiding errors in numerous real-world scenarios. Understanding conversion factors and their precise application ensures consistency and accuracy in diverse fields, from construction and trade to scientific research. The implications of inaccurate conversions can range from minor inconveniences to substantial structural or operational failures. Therefore, meticulous attention to conversion factors is essential to maintain reliability and accuracy in all measurement-based applications.

Frequently Asked Questions about 1.8m in ft

This section addresses common inquiries regarding the conversion of 1.8 meters to feet. Accurate understanding of these conversions is essential across various fields, ensuring consistency and precision in measurements.

Question 1: What is the approximate equivalent of 1.8 meters in feet?

1.8 meters is approximately equal to 5.905 feet. This conversion uses the standard conversion factor of approximately 3.28 feet per meter.

Question 2: Why is accurate conversion between meters and feet important?

Accurate conversion is crucial for various applications, including engineering design, architectural blueprints, construction, and scientific research. Discrepancies in conversion can lead to significant errors in these contexts, impacting the integrity and functionality of projects.

Question 3: What are the common pitfalls in converting between these units?

Common pitfalls include using incorrect conversion factors, misunderstanding the relationship between the units, and misapplying the conversion process to the specific context.

Question 4: How can I ensure accuracy when performing this conversion?

Accuracy is paramount. Employ standardized conversion factors, utilize reliable conversion tools or calculators, and maintain careful attention to the precision required by the specific application.

Question 5: In what situations might an approximation suffice, and when is precise conversion necessary?

Approximation may be sufficient for preliminary estimations or situations where high precision is not critical. However, precise conversion is necessary in applications requiring strict accuracy, such as engineering designs or scientific experiments.

Accurate conversions between units are crucial for maintaining consistency and avoiding errors across various disciplines. The conversion of 1.8 meters to feet exemplifies the importance of understanding and applying these conversions accurately. A thorough understanding of conversion factors and the specific requirements of each application ensures a reliable and precise outcome.

Further explore related topics on metric and imperial units to deepen your understanding of dimensional analysis.

Conclusion

The conversion of 1.8 meters to feet exemplifies the fundamental importance of accurate unit conversion. This seemingly simple calculation underscores the need for precise application of conversion factors to avoid errors in various fields. Key aspects explored include the relationship between metric and imperial systems, the significance of maintaining accuracy in different contexts, and the implications of approximation versus precise conversion. The process highlights the interconnectedness of measurement units and their critical role in fields from architecture and engineering to scientific research and global trade.

The exploration of "1.8m in ft" reveals the pervasive need for meticulous attention to detail in handling dimensional analysis. Maintaining accuracy in measurements is not merely a technical requirement; it safeguards against potential consequences ranging from miscalculations in construction projects to flawed conclusions in scientific studies. Understanding and practicing accurate conversion techniques remains crucial for the reliability and validity of diverse applications that depend on precise measurements. Continued awareness and application of these principles are essential for accurate, error-free results in any field leveraging dimensional quantities.