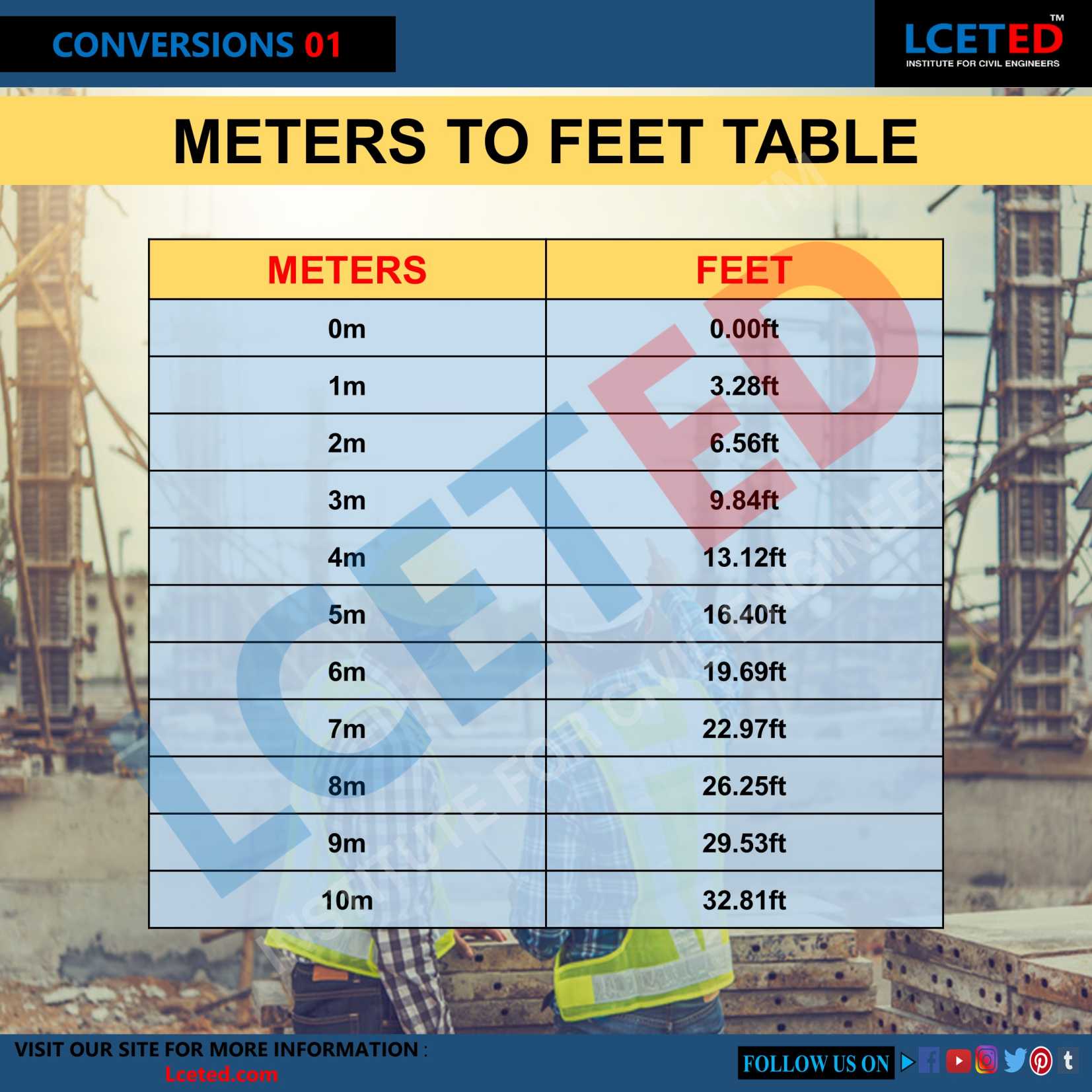
Converting Metric to Imperial: Understanding the Conversion of 1.8 Meters to Feet

Converting a measurement from meters to feet is a fundamental task in various fields. One common conversion is 1.8 meters. This conversion involves understanding the relationship between the metric system (meters) and the imperial system (feet). 1.8 meters is equivalent to approximately 5.9055 feet. This calculation is achieved by applying the conversion factor of 3.28084 feet per meter. Therefore, multiplying 1.8 meters by 3.28084 yields 5.9055 feet.

Understanding these conversions is vital for accurately interpreting measurements across different contexts. For example, in architecture and engineering, precise conversions are critical for blueprints and construction. In scientific research, consistent units are essential for accurate data analysis. The need to switch between metric and imperial measurement systems often arises in international collaborations, global trade, and travel. The accuracy of conversions directly impacts project planning, manufacturing, and even daily tasks. Maintaining precision in these calculations ensures consistency and reliability across disciplines.

This conversion is just one example of the numerous metric-to-imperial conversions. Further exploration into different conversion factors and their practical applications in various fields would provide a more comprehensive understanding of this aspect of measurement.

1.8m to Feet

Converting 1.8 meters to feet involves a fundamental understanding of unit conversions between the metric and imperial systems. Accurate conversions are crucial in various applications, from architecture to everyday measurements.

Conversion factor
Metric system
Imperial system
Measurement units
Approximate value
Precision
Applications
Accuracy

The conversion factor (3.28084) is the heart of the process. The metric system relies on meters, while the imperial system uses feet. Measurement units are crucial for clarity and accuracy. An approximate value (5.9 feet) is sufficient for many everyday applications, but precision is essential in fields requiring higher accuracy. Applications range from construction to scientific research. Accuracy ensures reliable results. Understanding these factors allows for appropriate application of the conversion.

1. Conversion factor

A conversion factor is essential for accurate measurements when transitioning between different unit systems. In the context of converting 1.8 meters to feet, this factor dictates the mathematical relationship between the two units. Its proper application ensures consistency and reliability in calculations.

Definition and Role
The conversion factor acts as a multiplier. It represents the ratio of one unit to another. In the case of meters to feet, the conversion factor reflects the inherent relationship between these units of length. It's a constant value that bridges the gap between the metric and imperial systems.
Calculation Application
To convert 1.8 meters to feet, one multiplies 1.8 by the conversion factor (3.28084). This mathematical operation precisely translates the measurement from one system to another. Failure to correctly apply this conversion factor will result in an inaccurate measurement. The process underscores the importance of accurate conversion factors for practical applications.
Precision and Accuracy
The precision of the conversion factor directly impacts the accuracy of the final measurement. A higher level of precision in the conversion factor leads to a more accurate conversion from meters to feet. Approximations may suffice in some cases, but for precise calculations, the precise conversion factor is indispensable.
Practical Application Examples
Accurate conversion factors are vital in engineering, construction, and various scientific contexts. Properly applying the conversion factor for measurements involving 1.8 meters is necessary in scenarios such as building design, material calculations, or scientific experiments. The use of conversion factors in these cases is essential.

In conclusion, the conversion factor is a critical component for converting 1.8 meters to feet. Its application ensures accurate results, which is essential in various real-world scenarios. Understanding the definition, calculation, precision, and application of the conversion factor clarifies the importance of this concept in measurement conversions.

2. Metric system

The metric system, a decimal-based system of measurement, underpins the conversion of 1.8 meters to feet. Its standardized units facilitate accurate and consistent measurements across disciplines. Understanding the metric system's structure is essential for comprehending the process of unit conversion.

Units of Measurement
The metric system employs a coherent set of units for length, mass, and volume, all derived from fundamental units like the meter, kilogram, and liter. The core principle is the use of prefixes, such as milli-, centi-, deci-, kilo-, to denote multiples and fractions of these fundamental units. This hierarchical structure allows for a wide range of measurements. The meter, the base unit of length, is a cornerstone in the conversion process from 1.8 meters.
Decimal Structure
The decimal nature of the metric system is crucial for conversions. Using decimals facilitates easy calculations by avoiding complex fractions. Converting between units involves multiplying or dividing by powers of 10. This inherent simplicity significantly simplifies the process of conversion between meters and feet. The consistent use of powers of ten streamline the process.
International Recognition
The international standardization of the metric system promotes universal communication in scientific, technical, and industrial contexts. This global recognition eliminates ambiguity in measurements and ensures consistency. The use of meters is universally understood, a crucial aspect of the conversion process from meters to feet. The global nature of this system underpins the universality of the conversion procedure.
Interrelation with Other Units
The metric system encompasses interconnected units. Relationships between units, such as meters and centimeters, are predetermined and integral to the system's design. Understanding these interconnections ensures accuracy and consistency in the context of conversions like 1.8 meters to feet. The interrelated nature of the system facilitates the use of the metric system across disciplines.

In conclusion, the metric system's standardized units, decimal structure, and global acceptance are foundational elements in the conversion of 1.8 meters to feet. These attributes are critical in many applications requiring a consistent and reliable unit system. The metric system's universality ensures the conversion is consistently applied.

3. Imperial system

The imperial system, a historical system of measurement, plays a crucial role in understanding the conversion of 1.8 meters to feet. Its inherent units, such as feet, are integral to the conversion process, necessitating a comprehension of the imperial system's structure and relationship to the metric system for accurate results. This connection is paramount for several reasons. Conversion involves understanding the established units and their relationship within the imperial system, enabling appropriate calculations. This understanding is essential for any circumstance demanding accurate measurement comparisons between the two systems.

Real-world applications highlight the significance of this understanding. For instance, blueprints for construction projects often incorporate imperial units. Precise conversions between imperial and metric systems are critical for ensuring compatibility and preventing errors in design and construction. Additionally, international collaborations, where metric and imperial measurements are used, necessitate the ability to convert efficiently. Without understanding the relationship between these systems, accurate conversions are impossible, leading to potential errors and misunderstandings. A clear grasp of the imperial system's units, in combination with knowledge of the metric system, ensures successful outcomes. This understanding is crucial in global trade and manufacturing as well. The historical influence of the imperial system, though gradually diminishing in certain contexts, necessitates ongoing comprehension for accurate conversions in various applications.

In summary, the imperial system is an integral component in the context of converting 1.8 meters to feet. Its units and the established conversion factors are essential for achieving precise results. This understanding is critical in numerous fields, requiring careful consideration of both systems for accurate comparisons and computations. The continuing use of imperial units in certain regions necessitates a strong understanding of their relationship to the metric system, particularly for converting quantities like 1.8 meters.

4. Measurement units

Measurement units are fundamental to the conversion of 1.8 meters to feet. The very act of expressing a quantity necessitates a unit of measure. Without defined units, a numerical value like "1.8" holds no inherent meaning. The meter and the foot represent distinct units of length within their respective systems. The metric system uses meters, while the imperial system employs feet. The conversion hinges on the relationship between these units. This relationship is established by a conversion factor. In essence, the choice of units dictates the procedure and outcome of the conversion.

Real-world examples underscore the critical role of measurement units. Construction blueprints rely on consistent units to ensure accuracy in building dimensions. Errors in specifying units can lead to significant discrepancies in a structure, highlighting the importance of maintaining the correct unit. In scientific research, standardized units are vital for data analysis and reproducibility. Inconsistency in units can undermine the validity of experiments. The very integrity of the results depends on using the correct units in all steps of the calculation, including those involving the conversion process. This is exemplified in calculating the length of a room, a necessary task involving unit considerations.

In conclusion, measurement units are an integral component of converting 1.8 meters to feet. The choice of units establishes the framework for the conversion process. Failure to acknowledge the significance of measurement units can result in errors, with repercussions in engineering, science, and numerous other fields. A deep understanding of units is essential for accurately expressing quantities in their respective systems, thereby ensuring correctness in calculations like the conversion from meters to feet. Consistent application of correct units is crucial for precise and reliable results.

5. Approximate value

The conversion of 1.8 meters to feet frequently necessitates an approximate value due to the inherent decimal nature of the conversion factor. The precise conversion involves a decimal fraction (3.28084 feet per meter). Calculating the exact value requires multiplying this factor by 1.8. However, the need for an approximate value arises in many contexts where the full precision is unnecessary or impractical. For instance, in everyday situations like estimating room dimensions or calculating material quantities, a rounded-off approximate value often suffices. Maintaining complete precision is not always required. The use of an approximate value often arises from the inherent limitations of practical applications and the specific level of precision needed in the context.

Real-world examples further illustrate this concept. Architectural sketches or preliminary engineering calculations may not demand the level of precision afforded by the full decimal conversion. A rounded-off value is adequate for initial design or planning. Similarly, if purchasing lumber for a project, an approximation of the needed lengths is sufficient for practical purposes. The crucial consideration is the degree of precision required for the given situation. In contrast, applications like high-precision manufacturing or scientific measurements necessitate the exact value, given the substantial impact even minute differences in measurements can have on the outcome. Choosing the appropriate level of precisionapproximation or exact valueis dictated by the specific context.

In summary, the use of an approximate value for conversions like 1.8 meters to feet stems from the practical need to balance accuracy with the context of the application. While the exact value is theoretically available, the approximate value often proves adequate and efficient for many everyday scenarios. The key lies in understanding the degree of accuracy required for different situations and selecting the appropriate approach to calculation.

6. Precision

Precision, in the context of converting 1.8 meters to feet, refers to the level of accuracy in the calculation. This accuracy is crucial for various applications, from architectural design to scientific experiments. The conversion between metric and imperial units inherently involves a conversion factor. Variations in the precision of this conversion factor directly impact the final result. Maintaining an appropriate level of precision is paramount to avoid errors that could have substantial consequences in practical applications.

Importance of Decimal Places
The number of decimal places retained in the conversion factor significantly influences the precision of the final result. Using a less precise conversion factor will lead to a less precise result. For instance, rounding the conversion factor to 3.3 might be acceptable for a preliminary estimate but is insufficient for detailed calculations. In contrast, using the full conversion factor, potentially retaining many decimal places, is crucial for high-precision applications.
Impact on Real-World Applications
The level of precision required varies widely depending on the context. In everyday scenarios, a basic approximation might suffice. For instance, determining a general room size can be accomplished with limited precision. However, in engineering or scientific applications, the need for greater accuracy is paramount. Inaccurate measurements for bridge construction or chemical experiments could have severe consequences, highlighting the direct correlation between precision and safety or reliability in various fields. Thus, accuracy directly impacts safety, precision, and efficiency.
Relationship to Conversion Factors
The chosen conversion factor profoundly dictates precision. Employing a conversion factor with more decimal places inherently yields a more precise result. The conversion factor, representing the ratio between meters and feet, directly determines the precision of the calculation. The use of a conversion factor with a higher number of digits after the decimal point directly translates to greater accuracy in the final result. This demonstrates the interplay between conversion factors and precision in the process of converting 1.8 meters to feet.
Balancing Accuracy and Practicality
The ideal precision level necessitates a balance between accuracy and practicality. Extreme precision may be unnecessary and computationally intensive for many common tasks. Excessive decimal places often add complexity without significantly altering the outcome. The challenge is choosing a level of precision that balances the need for accuracy with the practical constraints of a specific situation. The correct use of precision is vital for ensuring efficiency, accuracy, and reliability within the context of converting 1.8 meters to feet.

In conclusion, precision in the conversion of 1.8 meters to feet is paramount. Understanding the intricate connection between decimal places, conversion factors, and real-world implications is vital to making appropriate choices based on the specific application. This appreciation of the need for accuracy allows for responsible and effective application of the conversion in diverse contexts.

7. Applications

The conversion of 1.8 meters to feet, while seemingly a simple mathematical exercise, finds practical application across diverse fields. Accurate conversion is essential for ensuring compatibility between systems and avoiding errors that can have substantial consequences. The application of this conversion is fundamentally linked to the need for consistent measurements across different contexts. A clear understanding of this conversion, particularly in fields requiring precise calculations, is crucial.

Real-world applications are numerous. In architecture and engineering, blueprints often utilize imperial units (feet) for design and construction. When dealing with international collaborations or projects involving foreign partners, accurate conversions between metric and imperial systems are indispensable for seamless communication. Failure to correctly convert 1.8 meters to feet in such instances could result in significant discrepancies in design and subsequent construction, impacting the project's budget, timeline, and ultimately, its success. Similarly, in manufacturing and industrial settings, consistent measurements are critical to ensure component compatibility and prevent costly errors. Correctly converting 1.8 meters to feet ensures adherence to specifications, mitigating potential malfunctions or quality issues. The need for accurate conversion applies equally to scientific research, where consistent unit systems are vital for data analysis and reproducibility. This is exemplified by the requirement for accurate conversion factors when performing experiments or comparing data from various sources, ensuring the reliability of conclusions derived from the research.

Understanding the practical implications of converting 1.8 meters to feet is crucial. The application of accurate conversions extends beyond specific projects and underscores the importance of understanding the interconnectedness of different measurement systems. This principle is applicable to any field that requires a transition between metric and imperial measurements, highlighting the need for a standardized approach. The ability to correctly convert values like 1.8 meters to feet demonstrates a fundamental skill for anyone engaged in activities requiring precise calculations or interactions with diverse measurement systems. Consistent understanding and application of this conversion support smooth operations in a wide array of fields, from engineering and manufacturing to scientific research and international cooperation.

8. Accuracy

Accuracy in the conversion of 1.8 meters to feet is paramount. A precise conversion is foundational to various applications, from architectural design to scientific experiments. Errors in this seemingly simple calculation can cascade into significant discrepancies in subsequent analyses and implementations. The conversion's accuracy is directly linked to the reliability and efficacy of any process employing the converted value. A minor error in the conversion of 1.8 meters can lead to substantial errors in related calculations, necessitating a meticulous and precise approach.

Real-world examples underscore the critical importance of accuracy. In construction, inaccurate conversions can lead to structural issues, compromising safety and potentially resulting in costly repairs or even catastrophic failures. In engineering, a slight error in converting 1.8 meters might affect component fit, potentially causing malfunctions in machinery or equipment. Even in scientific research, inaccuracies in conversion can invalidate experimental data, leading to flawed conclusions. This emphasis on precision underscores the need for meticulous attention to detail in calculations involving unit conversions. Maintaining accuracy throughout the conversion process is vital to ensure reliable outcomes across different applications. This meticulous approach extends beyond the immediate conversion, influencing the precision and validity of subsequent computations.

In conclusion, accuracy in the conversion of 1.8 meters to feet is not merely an academic exercise; it is a practical necessity. The potential consequences of inaccuracy in various applications, from construction to scientific research, highlight the importance of meticulous attention to detail and rigorous methodology in all conversion processes. Accurate conversions are fundamental to ensuring the reliability, safety, and validity of diverse applications, demonstrating the profound implications of precision in unit transformations. This underscores the critical importance of accurate conversions in ensuring the integrity and success of a wide range of projects and endeavors.

Frequently Asked Questions

This section addresses common queries regarding the conversion of 1.8 meters to feet. Accurate conversion between metric and imperial units is crucial for various applications, and this FAQ aims to clarify common misconceptions.

Question 1: What is the precise conversion of 1.8 meters to feet?

The precise conversion of 1.8 meters to feet is approximately 5.9055 feet. This value is derived by multiplying 1.8 meters by the conversion factor of 3.28084 (feet per meter).

Question 2: Why is a precise conversion important?

Precision in conversion is crucial across diverse fields. Inaccurate conversions in architectural design, engineering calculations, or scientific experiments can lead to significant errors, impacting project timelines, budgets, and, in some cases, safety. The accuracy of conversions ensures reliable outcomes.

Question 3: How does the conversion factor work?

The conversion factor represents the established ratio between units. In this case, the factor (3.28084) reflects the relative size of a foot compared to a meter. Multiplying the measurement in meters by this factor yields the equivalent measurement in feet. A clear understanding of this factor is essential for accurate conversions.

Question 4: When is an approximation sufficient for converting 1.8 meters?

An approximation might be sufficient in everyday contexts or preliminary estimations. However, for precise applications such as engineering blueprints or scientific studies, maintaining the full precision of the conversion is essential to avoid potentially significant errors. The context dictates the level of accuracy required.

Question 5: What are the broader implications of converting between units?

Conversion between different units, like meters and feet, is crucial for seamless communication and collaboration in a globalized world. Understanding these conversions ensures clarity and consistency across different systems of measurement. Consistency in units is paramount in various applications, from international trade to scientific research.

Understanding these FAQs clarifies common aspects related to converting 1.8 meters to feet, highlighting the importance of precision in various contexts. For further information, refer to established resources on unit conversion methodologies.

Next, we will explore the historical context of measurement systems.

Conclusion

The conversion of 1.8 meters to feet underscores the fundamental importance of accurate unit conversions. This process, reliant on established conversion factors and a clear understanding of both the metric and imperial systems, is crucial across various fields. Key elements explored include the precise conversion calculation, the significance of the conversion factor, the historical context of measurement systems, the importance of precision, and the various practical applications of this conversion in fields like construction, engineering, and science. The discussion highlights how seemingly simple conversions are inherently complex, demanding meticulous attention to detail and a thorough comprehension of the underlying principles.

The conversion of 1.8 meters to feet, while a fundamental task, serves as a microcosm of broader challenges in measurement consistency and cross-system compatibility. Maintaining accuracy in these conversions is essential for effective communication, collaboration, and the avoidance of potentially costly errors. A robust understanding of unit conversions is vital in an interconnected world, ensuring reliable outcomes in various professional and scientific domains.